Introduction
I think that every security researcher has a couple of vulnerabilities that sit close to their heart, those that marked a turning point in their trajectory or taught them something crucial about security. For me, one of those vulnerabilities is the padding oracle attack.
There’s plenty of excellent information about padding oracle attacks out there, but it’s scattered across different blog posts, forums, and articles. On top of that, some of the sources conflict with each other, which be confusing for those trying to understand this technique.
There’s also a lack of tools to conduct this attack, so I decided to create my own!
I called it Delphi, named after Pythia, the Oracle of Delphi. It’s a Python library that you can plug into your own proof-of-concept scripts and customize for the target you’re working on.
In this post, I’ll share what I know about padding oracle attacks, focusing on how they work with AES in CBC mode and PKCS#7 as the padding standard. I’ll go over how the attack works, why the potential security impact, and how to use Delphi to pull it off.
Crypto 101
For those not well-versed in cryptography, there are some fundamental concepts we need to cover to make sense of this attack.
That being said, I am not a cryptography expert. I recommend checking the resources section for explanations from people who are much more proficient at cryptography than I am.
What I’ll cover here is just the absolute minimum you need to know. Specifically, the concepts of block ciphers, padding, and CBC. If you already familiar with these topics, feel free to skip ahead.
Block Ciphers & Padding
AES, like most modern symmetric encryption algorithms, is a block cipher. Block ciphers split the message you want to encrypt or decrypt into chunks of fixed-size bytes, called blocks. The block size depends on the algorithm in question. AES, for example, uses 16-byte blocks.
However, it’s possible that a message won’t perfectly fit into the blocks. For instance, a message that is 30 bytes long, split into 16-byte blocks, will leave 2 bytes of unused space in the second block.
We can’t have blocks smaller than the fixed amount prescribed by the algorithm, or the encryption won’t work. Nor can we leave the empty space filled with zeros, because how would we distinguish between the zeros that are actually part of the message and empty space?
That’s where padding standards come in!
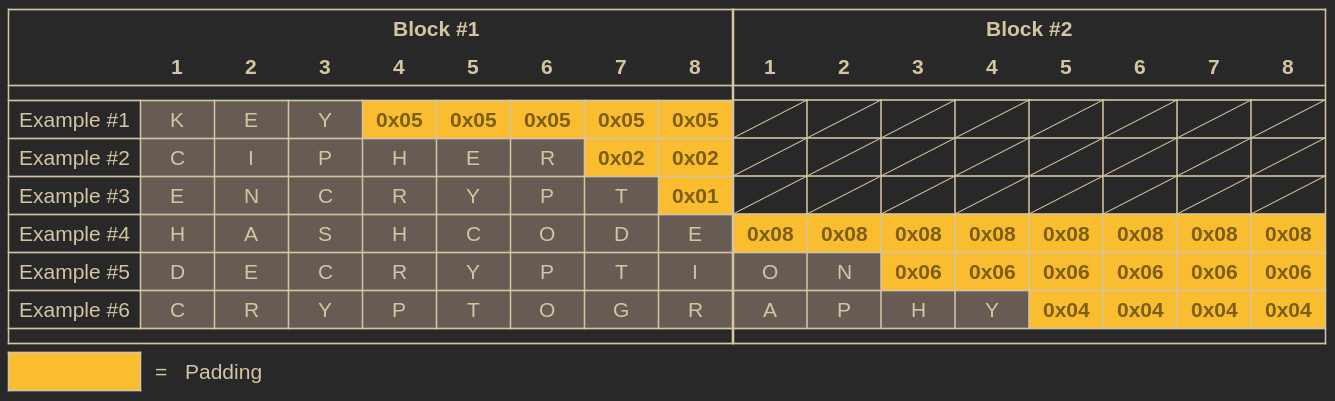
Examples of message padding. Note that in this example blocks are 8 bytes long, not 16 like in AES.
The most popular modern padding standard is PKCS#7, and that’s the one we’ll focus on today.
In simple terms, PKCS#7 defines that trailing empty space in a block is filled with padding bytes equal to the number of bytes needed to fill up the remaining block. If that sounded complicated, just remember that if there are N spaces left in the block, PKCS#7 fills this space with N bytes, all having the value N.
So, for an AES ciphertext to be compliant with PKCS#7, it must end with one of these patterns:
- One 0x01 byte:
[..., 0x01] - Two 0x02 bytes:
[..., 0x02, 0x02] - Three 0x03 bytes:
[..., 0x03, 0x03, 0x03]
…and so on until…
- Sixteen 0x10 bytes:
[0x10, 0x10, 0x10, 0x10, 0x10, 0x10, 0x10, 0x10, 0x10, 0x10, 0x10, 0x10, 0x10, 0x10, 0x10, 0x10]
Yes, even if a message perfectly fits into a block without empty space, we still need to add another block filled entirely with padding. Every ciphertext must have a padding (just look at the “HASHCODE” exaple in the previous image).
On most cryptographic libraries, trying to remove the padding from a ciphertext or plaintext that doesn’t have valid padding (i.e., one that doesn’t end in one of these sequences) will cause an exception to be thrown. This is an important detail that will be critical in executing the padding oracle attack.
Cipher Block Chaining
The reason why messages get split into blocks is because, as the name implies, block ciphers perform encryption and decryption operations on a block-by-block basis. But as we saw, sometimes messages end up being more than one block long.
The way a block cipher handles operations with messages made of multiple blocks is determined by the mode of operation. The most naive mode of operation would be to treat each input block independently and simply join the resulting blocks at the end. This mode of operation is called Electronic Code Book (ECB).

Illustration of how ECB encryption works. The decryption process is the same but in reverse.
Note about figures
These figures are simplified for clarity. Note:
- They use 4-byte blocks for readability. Real AES uses 16-byte blocks, which would be unwieldy for demonstration purposes.
- The byte values shown are arbitrary and may not accurately represent real XOR operations.
However, this mode is insecure. By treating the blocks independently and not as part of a whole, plaintext blocks of the same value will produce the same ciphertext block. This creates patterns in the ciphertext that reveal information about the plaintext, which is unacceptable on most circumstances.

Visualization of how ECB leaks patterns in the plaintext. Left is original (plaintext), right is encrypted (ciphertext).
But we are not here to talk about ECB. The padding oracle attack is related to the Cipher Block Chaining (CBC) mode.
CBC aims to fix this issue with ECB by introducing a clever trick: before encrypting a block of plaintext, we XOR it with the previous block’s ciphertext.
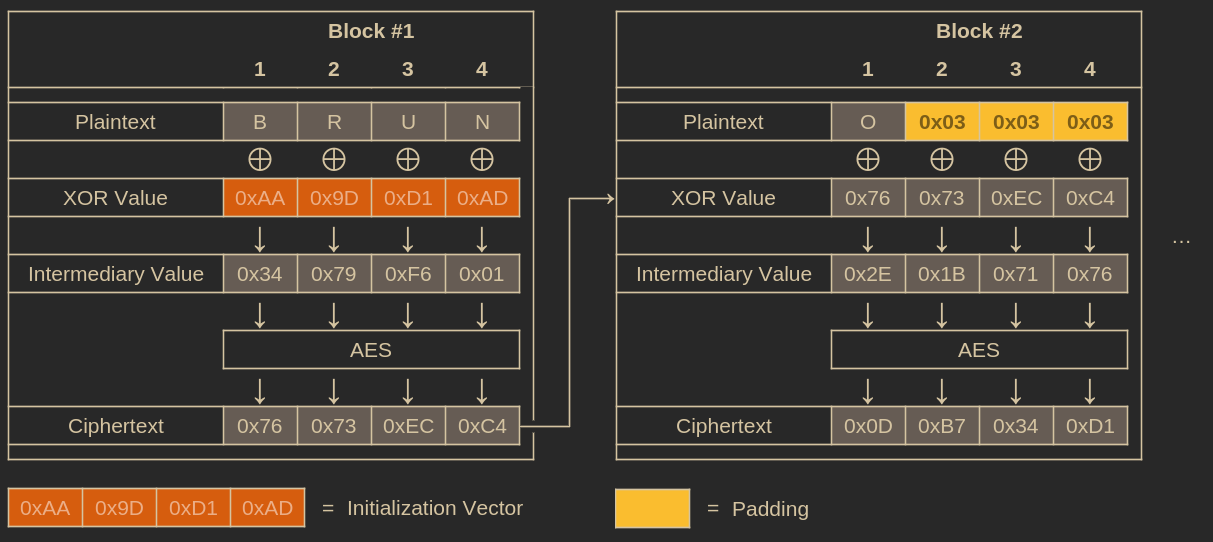
Illustration of how CBC encryption works.
Of course, in the case of the very first plaintext block, there isn’t a previous block of ciphertext for us to XOR with. Instead, we XOR it with something called an Initialization Vector (IV), which is just a block of random data generated for each message. When we share the encrypted message, we also share the IV. Think of it as the 0th block of the ciphertext.
CBC employs this technique to introduce randomness into the encryption process, ensuring that identical plaintext blocks do not produce identical ciphertext blocks. Even if the plaintext block is the same, the XOR value won’t be, which ensures a different input to the AES function.
The decryption process, which is actually more important for understanding this attack, mirrors the encryption process but works in reverse:
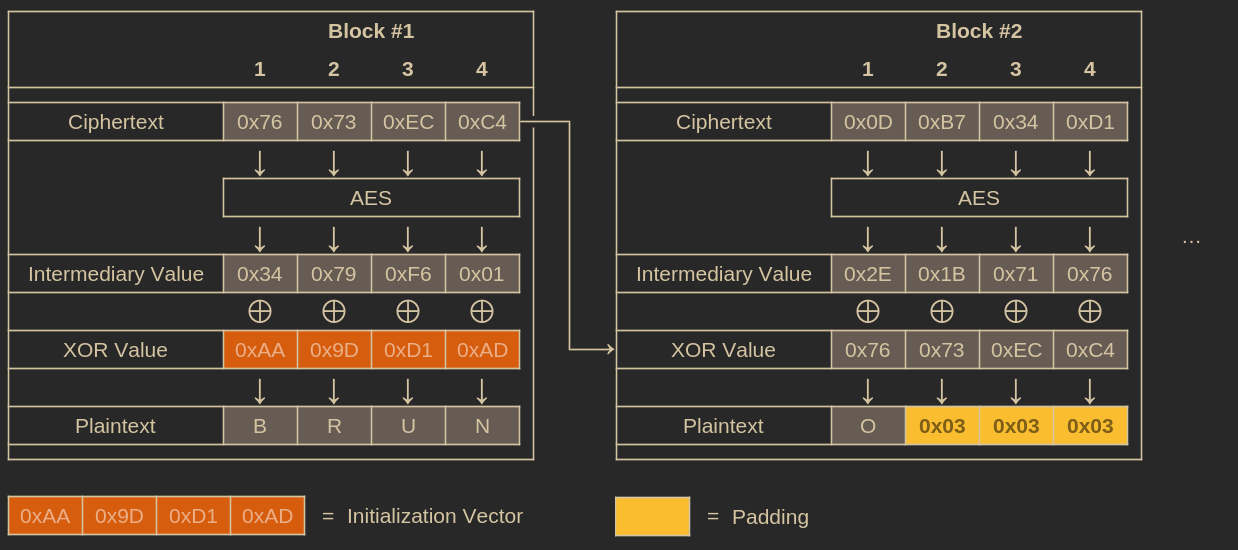
Illustration of how CBC decryption works. Notice the valid padding.
While chaining ciphertext and plaintext blocks together fixes the pattern leakage issue of ECB mode, it introduces new vulnerabilities.
For example, during the decryption process, you’ll notice that altering the value of a plaintext byte is possible by modifying the corresponding byte in the previous block’s ciphertext. For the first block, which doesn’t have a previous block, you modify the IV.
This might not seem like a big deal right now, but it’s actually a key part of the padding oracle attack. Here’s the important information to remember about CBC mode:
- During decryption, CBC will XOR the intermediary value of a block with the previous block’s ciphertext.
- The IV is a special block sent alongside the ciphertext that serves as the XOR value for the first block.
- This allows modification of a block’s plaintext by tampering with the previous block’s ciphertext (or the IV in the case of the first block).
Attack Explanation
Now that we’ve covered the basic cryptography concepts needed to understand this attack, let’s dive into how it works.
If you’re already familiar with this type of attack, feel free to skip ahead to learn how to use my tool for decryption and encryption exploits.
Scenario
To better illustrate a scenario where a padding oracle attack might be used, let’s consider a hypothetical vulnerable web application. Please ignore the million other ways this example is a security nightmare and just focus on what matters for the attack.
Imagine an online gambling site, but it’s a really basic one that only offers a coin toss game (calling heads or tails).

I’ve created the source code for the API this website would use, which you can check in full here. Let’s break it down to understand how it works.
To place a bet, a user must first obtain a token by making a GET request to the endpoint /get_token.
@app.route('/get_token', methods=['GET'])
def get_token():
name = get_player_name()
next_result = random.choice(['HEADS', 'TAILS'])
token = encrypt_and_encode(name, next_result)
return f"Your token is: {token}", 200
This endpoint generates a token containing the player’s name and whether the result of the next game will be heads or tails. This information is stored as a comma-separated string and encrypted using a server-side encryption key, which is unknown to the player.
The token ciphertext, prepended by the IV used for encryption, is base64 encoded and returned to the player. Naturally, the player wouldn’t know the contents of the token.
After receiving the token, the player can now gamble by making a POST request to the /gamble endpoint, providing the token and their guess of heads or tails.
@app.route('/gamble', methods=['POST'])
def gamble():
data = request.json
bet = data.get('bet')
token = data.get('token')
decoded_token = decrypt_and_decode(token)
try:
name, next_result = decoded_token.split(',')
except:
return "Sorry, your token is malformed!",401
if bet == next_result:
increase_balance(name, PRIZE_MONEY)
return "You win!", 200
else:
reduce_balance(name, COST_TO_PLAY)
return f"Better luck next time, {name}!", 200
This endpoint performs several tasks. First, it decrypts and decodes the token using the same key used on encryption. If the provided token was not encrypted with the server-side key, then this would fail.
Then, the player’s name and the result of the incoming game are extracted from the now-plaintext token. If this extraction fails due to a malformed token, the endpoint will respond with a status code of 400 (Bad Request).
Finally, the endpoint compares the player’s bet with the result of the game, which was already determined when the token was generated. If the player guessed correctly, a prize is added to their wallet. Otherwise, they lose money.
The Vulnerability
Since the /gamble endpoint only accepts tokens generated with the server’s encryption key (a secret unknown to users) it seems impossible for users to forge tokens. This should mean they can’t cheat the game or make bets on behalf of other players. Any information in a valid token should be trustworthy since the only way for it to exist is if the server itself created it.
The developers might have implemented this in a somewhat unconventional way, but at first glance, it seems secure, right?
Not so fast. We need to take a closer look at how the decrypt_and_decode function handles the token decryption.
def decrypt_and_decode(token : str):
# Decode the Base64-encoded token to bytes
token_bytes = base64.b64decode(token)
# Extract the IV (first 16 bytes) and ciphertext
iv = token_bytes[:AES.block_size]
ciphertext = token_bytes[AES.block_size:]
# Initialize AES cipher in CBC mode
aes = AES.new(ENCRYPTION_KEY, AES.MODE_CBC, iv)
# Decrypt and unpad the plaintext
plaintext = aes.decrypt(ciphertext)
plaintext = unpad(plaintext, AES.block_size)
# Decode plaintext from bytes to string
decoded_token = plaintext.decode("utf-8", errors='replace')
return decoded_token
The cryptographic setup is fairly standard. AES in CBC mode is used as the algorithm, with a 256-bit key. After decryption, the unpad function is used to strip the padding from the decrypted plaintext. By default, the unpad function uses PKCS#7 as the padding mode.
PKCS#7 requires padding to follow a specific format to be considered valid, as we saw previously. If a random ciphertext, not generated with the encryption key, is provided for decryption, the resulting plaintext will most likely have invalid padding simply by a matter of chance.
So, how does the unpad function handle a plaintext with invalid padding when a forged ciphertext is provided?
As documented here, the unpad function raises a ValueError exception if it encounters invalid padding in the plaintext. Since this exception isn’t handled by the code, the endpoint function will terminate and return a status code of 500 (Internal Server Error).
This behavior is critical for our attack. Let’s break down what the endpoint’s status code tells us about the ciphertext we provided:
- 400: The ciphertext decrypted into a plaintext with valid padding, but the plaintext token was malformed.
- 200: The ciphertext decrypted into a plaintext with valid padding, and the game was played.
- 500: The ciphertext decrypted into a plaintext with invalid padding, triggering an exception and causing the server to error out.
From this, we can deduce the following:
- If the decrypted ciphertext has valid padding, the status code is either 400 or 200.
- If the decrypted ciphertext has invalid padding, the status code is 500.
This might not seem like much at first, but it represents a massive leak of information.
This endpoint effectively acts as an oracle, revealing to us whether the decryption of the ciphertext we provided results in valid padding. This is the titular padding oracle. And just like a mythical oracle that can access privileged knowledge from the gods, we can use the information revealed by our padding oracle to our advantage.
Other type of oracles
That’s not to say the padding oracle in this example is the only way an oracle can exist.
In the most general sense, a padding oracle is any interaction with the target system that lets you deduce the plaintext’s padding validity of a ciphertext you provided based on its behavior. The specific “tell” that reveals this information can vary widely.
For example, the tell might not be in the status code, it could be in a header or the body of the response message. Perhaps the oracle isn’t even an API endpoint. It could be a system that outputs a log message or changes its behavior in another detectable way.
A famous example of a padding oracle attack is the Lucky Thirteen attack, which targeted certain implementations of the TLS protocol. Instead of relying on status codes or direct responses, it exploited timing differences in the server’s responses to deduce the validity of the padding. This is an example of a side-channel padding oracle.
To clarify, here are the conditions required for a padding oracle attack to be possible:
- The target system must receive arbitrary ciphertexts (and IVs) from the attacker and attempt to decrypt it and remove the resuling plaintext’s padding.
- The attacker must be able to deduce whether the ciphertext decrypted to something with valid padding (the padding oracle).
- The symmetric encryption algorithm in use must be AES operating in CBC mode.
- A predictable padding scheme, such as PKCS#7, must be used to strip the padding during decryption.
- There must be no additional integrity checking measures in place, such as the use of a Message Authentication Code (MAC).
Impact
By now, we’ve covered the conditions that enable padding oracle attacks, but we haven’t yet explored how they work or what can be accomplished with them.
We’ll dive into the specifics in the next two sections, but broadly speaking, there are two types of padding oracle attacks:
- Decryption attack: The attacker can uncover the plaintext for any ciphertext encrypted with the oracle’s encryption key.
- Encryption attack: The attacker can create a valid ciphertext for any arbitrary plaintext they choose, which will decrypt correctly using the oracle’s key.
The impact of a decryption attack is straightforward: any sensitive information encrypted with the server-side key can be exposed if the attacker gets a hold of the ciphertext. Examples of such sensitive information might include login tokens, API keys, or user data.
The impact of an encryption attack depends entirely on what the target system does with the decrypted plaintext, that is, the “sink” where the input ends up. For example:
- If it passes the plaintext as an argument to a function like
os.system(), you’re looking at a Command Injection scenario. - If the target system uses the decrypted plaintext to load a file, this could lead to a Local File Inclusion (LFI) or Path Traversal vulnerability.
- If the plaintext is used to build a SQL query, that could lead to SQL Injection.
The possibilities are nearly limitless, depending on how the system processes the decrypted plaintext.
In general, this approach of trusting encrypted information hinges on a critical assumption: because the encryption key is a server-side secret, the system treats any information encrypted with it as inherently trustworthy. This trust may lead the system to skip additional authentication checks.
By forging ciphertexts, we exploit this trust and create a channel for privileged interaction with the target system, which can be leveraged for some very powerful exploits.
Not being able to control the IV
Previously, I listed the ability to control the IV as a prerequisite for a successful padding oracle attack, but that’s not necessarily true.
As discussed, the IV is essential for correctly encrypting and decrypting in CBC mode. Without it, we couldn’t perform operations on the first block of plaintext. As the IV modifies the first block’s plaintext, the same IV must be used for both the encryption and decryption of a given message to ensure proper decryption.
Typically, to add randomness (a key purpose of the IV), we generate a new IV for each message. This IV is then shared alongside the ciphertext, usually prepended as a 0th block. When time for decryption comes, the user will provide both the IV and the ciphertext to the system. You can see in the source code that this is what the API does.
However, there’s another possibility: instead of generating a new IV for each message, we could use a constant, hardcoded IV for all encryption and decryption operations. In this case, the encrypted message wouldn’t need to include the IV, as it’s always the same and embedded in the code.
Hardcoding an IV is generally considered bad practice in cryptography. But ironically, in this case, it works against a padding oracle attack. Without the ability to provide the IV, attackers lose control over the first block. However, we can still control subsequent blocks because the first ciphertext block (which we do control) will be XOR’d into the following block and so forth in a chain.
This is what it means in practice:
- During decryption attacks: We won’t be able to decrypt the first ciphertext block. It will remain gibberish.
- During encryption attacks: We can forge a ciphertext for any plaintext we want, but it will always be prepended with a block of garbage data.
These limitations could potentially derail an attack. For example:
- If the critical information in a ciphertext resides in the first block, we wouldn’t be able to decrypt it.
- If the target system expects a specific format (like a valid URL) in the plaintext, the garbage block could render our forged message invalid.
That said, in some cases, these limitations might not matter:
- Decrypting the blocks after the first might still yield valuable information.
- A random block at the start of our plaintext might not interfere with the attack.
So, even without IV control, a padding oracle attack could still be viable. As an exercise, consider whether the attack I’ll outline in this post could still work if the IV were hardcoded.
Delphi has support for attacks with and without IV control.
What about the encryption key?
This talk about the attack being used to decrypt and encrypt data with the server-side encryption key might give the impression that we’ve somehow compromised the key itself. But that’s not the case.
As we’ll see when we delve deeper into the attack, at no point are we retrieving the actual value of the key. Instead, we’re abusing the target to perform decryption operations on our behalf using ciphertexts we provide and consulting the oracle to determine if the result has valid padding. By leveraging this information, we can brute force the plaintext of a given ciphertext or even forge our own ciphertexts.
In essence, the attack grants us the ability to perform encryption and decryption operations with the key without ever learning its value. You might wonder if we could eventually deduce the encryption key by collecting enough ciphertexts and their corresponding plaintexts. However, modern algorithms like AES are specifically designed to resist such known-plaintext attacks, as explained here.
That said, there’s one fun exception. If instead of generating a new IV for every message, the oracle uses a constant IV that is equal to the encryption key, we can perform an attack where we work out the IV value, and thus, discover the encryption key. This seems like a huge oversight, and I’m not sure how common it is to encounter in the wild, but this blog post explains how the attack works.
Decrypt A Message
We can now finally talk about how a decryption padding oracle attack works. We’ll first cover how it works theoritically by explaining the cryptography principles, then I’ll explain how to make a PoC against the gambling API using Delphi.
Let’s revisit the gambling site example. Previously, we made a request to the /token endpoint and received a Base64-encoded token. In the source code, we can verify that this token comprises the ciphertext bytes prefixed by the IV.
When we send a request to /gamble with the token, the server decrypts the ciphertext using the provided IV, unpads the resulting plaintext, and performs some operations based on it.
Let’s see how an attacker might conduct a padding oracle attack to decrypt their token.
Let’s outline what we know and what is unknown to an attacker. For simplicity, assume the ciphertext consists of a single block.

Bytes we don't know the value of have question marks.
Here’s what we know:
- The XOR value (since this is the IV, the first 16 bytes of the token).
- The ciphertext bytes (the remaining bytes of the token).
What we don’t know:
- The intermediary value (as we lack the decryption key to perform the AES function).
- The plaintext (which is the goal of this attack).
Now, suppose we send a forged token to the /gamble endpoint. We start with a legitimate token from the /token endpoint but modify it by replacing the first 16 bytes (the IV) with custom values. This means we’re submitting the same ciphertext as before but with a different IV.
Let’s try submitting an IV filled with all zeros alongside our ciphertext. What do you think will happen?

Bytes we don't know the value of have question marks.
What will in all likelihood happen is that, regardless of the intermediary value generated by AES decrypting the ciphertext, when it is XOR’d with our custom IV, the resulting plaintext will not have valid padding, as it would be gibberish data. If this occurs, our oracle will notify us by returning a 500 status code, as we’ve discussed.
Here’s where the fun begins: what would it take for this gibberish plaintext to have valid padding?
As we discussed earlier, PKCS#7 padding considers a trailing sequence of \(n\) bytes with value \(n\) as valid. The smallest valid padding is a single byte of 0x01 at the end of the block.
We don’t know the value of the last plaintext byte, but we know it results from the XOR operation between:
- The last byte of the intermediary value.
- The last byte of the IV.
Mathematically, there must exist an IV byte value that, when XORed with the last intermediary byte, results in 0x01.
To find this, we can increment the last byte of our all-zeros IV from 0 to 255, sending the modified IV alongside the original ciphertext to /gamble each time. We continue until we stop receiving a 500 status code.

Performing a brute-force attack until we stop receiving a padding error.
When the server stops returning a 500 status and responds with something else, it means the plaintext has valid padding ending in [..., 0x01].
We should now repeat the process for the second-to-last byte. But first, we need to make sure our last byte (which we just brute-forced) decrypts to 0x02 instead of 0x01. To do that, we must determine the last byte of the intermediate value, which we can obtain by XORing the brute-forced value with 0x01.
Next, XOR the discovered last byte of the intermediate value with 0x02 to get the correct value for the last byte of the IV that will produce 0x02 in the last byte of plaintext. Now we can start brute-forcing the penultimate byte until the server stops returning a 500 status, which indicates we’ve found valid padding of [..., 0x02, 0x02].
By repeating this process for all bytes of the IV from right to left, we will eventually discover an IV that, when combined with the ciphertext, yields a plaintext consisting entirely of padding.

After performing the brute-force attack, we arrive at a plaintext full of padding.
The [..., 0x02, 0x02] Edge Case
There’s actually a small edge case we need to consider when performing this brute-force attack.
Let’s assume we’re still trying to brute-force the last byte of the IV. However, unbeknown to us, the penultimate byte of the plaintext is set to 0x02.
Now, what happens if, while testing different values for the IV’s last byte, we end up with 0x02 as the last byte of the plaintext before 0x01? In that case, the padding would be valid as [..., 0x02, 0x02], but we might mistakenly think it’s [..., 0x01].
This is why, when we get a positive response from the oracle while brute-forcing the last byte, we need to perform an additional check. Fortunately, this check is simple: we increment the penultimate byte of the IV and verify if the padding is still valid.
If the padding remains valid, it means the padding is [..., 0x01] and we can now brute-force the penultime byte and so on.
If it’s no longer valid, then the padding was actually [..., 0x02, 0x02], and we’ll need to keep searching for the correct value for the last byte of the IV.
At first glance, this might seem unhelpful since the plaintext derived using the bogus IV is not the actual plaintext we want. However, this step is critical.
Look at the result: the only unknown is the intermediary value. This value represents the ciphertext after the AES decryption step and remains the same regardless of the IV used.
Recall the intermediary value’s relationship with the XOR value and the plaintext:
$$ \text{Intermediary Value} \oplus \text{XOR Value (our IV)} = \text{Plaintext} $$Since XOR operations are reversible:
$$ \text{Plaintext Value} \oplus \text{XOR Value (our IV)} = \text{Intermediary Value} $$Now that we know both the plaintext (a blockful of padding) and our custom IV, we can calculate the intermediary value. Again, I emphasize that this value is constant for the ciphertext, regardless of the IV.
One simple XOR operation later, and we now know the intermediary value for the cipher. Let’s return to assessing what we know about the message we want to crack with the real IV.

Now we know the intermediary value.
At this point, the attack is almost complete. As you’ll remember:
$$ \text{Intermediary Value} \oplus \text{Xor Value (the real IV)} = \text{Plaintext} $$By performing a simple XOR operation between the legitimate IV and the discovered intermediary value, we can recover the real plaintext for our token.

The plaintext is revealed! Notice the valid padding.
The attack procedure is essentially the same if the ciphertext we want to crack consists of multiple blocks. We would start with the first block, perform the attack as described, and then move on to the next block, and so on. The only difference is that after the first block, we use the previous block’s ciphertext instead of the IV as the XOR value.
If you’re interested in seeing how this attack can be implemented in Python, check out the source code for Delphi. The _get_intermediary_value function handles the brute-forcing to recover the intermediary value for a block, which is then used by the decrypt function to conduct the attack on the ciphertext.
Here’s how you can leverage Delphi to create a PoC for exploiting the gambling site:
- Download a local copy of
delphi.pyfrom the GitHub repository. - In the same directory, create your own Python script.
- Import the
decryptfunction from Delphi. - Define a padding oracle function that interacts with the target, returning
TrueorFalsedepending on the padding’s validity. - Extract the IV and ciphertext from the token you want to crack.
- Call the
decryptfunction with the IV, ciphertext, and oracle function as arguments.
This is the PoC I came up with:
from delphi import decrypt
import base64
import requests
from Crypto.Util.Padding import unpad
# API service
URL = 'http://127.0.0.1:5000'
# Oracle function
# Makes POST request to /gamble with token and evaluates response
# Return True if padding is valid, False if not.
def ask_oracle(iv : bytes, ciphertext : bytes) -> bool:
token = base64.b64encode(iv + ciphertext).decode('utf-8')
data = { "token" : token, "bet" : "WHATEVER"}
response = requests.post(f"{URL}/gamble", json=data)
if response.status_code == 500:
return False
else:
return True
# Token we want to crack
token = 'iURdnlEGAreK/ovx7v78PtkUhvBn1/fchcm1k9Nig1g='
# Extract IV and ciphertext from token
token_binary = base64.b64decode(token)
iv = token_binary[:16]
ciphertext = token_binary[16:]
# Conducts decrypt attack using Delphi to retrieve plaintext
plaintext = decrypt(iv, ciphertext, ask_oracle)
# Removes padding from the plaintext and prints it
plaintext = unpad(plaintext, 16).decode('utf-8')
print(plaintext)
If you run the PoC, you should see the recovered plaintext from the token in a few seconds. To output progress, set the DEBUG variable in delphi.py to True.
[user@mydesktop ~]$ python poc.py
Reader,TAILS
At this point, the attacker will have successfully discovered the contents of the encrypted token and will never lose a coin toss again.
[user@mydesktop ~]$ curl -X POST \
-H "Content-Type: application/json" \
-d '{
"bet": "TAILS",
"token": "iURdnlEGAreK/ovx7v78PtkUhvBn1/fchcm1k9Nig1g="
}' \
'http://127.0.0.1:5000/gamble'
You win!

Encrypt Your Own Message
Now let’s move on to the encryption padding oracle attack. Like before, we’ll first cover the cryptography behind it, and then I’ll show you how to make a PoC against the gambling API using Delphi.
Most of the information you’ll find online about padding oracles focuses on the decryption attack, with very few examples of code for the encryption attack.
I’m not sure why, but many sources overlook the encryption aspect. In fact, during my research, I came across cryptography forum posts claiming that it’s not possible to forge ciphertexts using padding oracles, or that it only works for specific plaintexts or if you have a valid ciphertext to base it on.
But as far as I know, you can absolutely exploit a padding oracle to forge your own ciphertext for any arbitrary message you want. There’s no limitation on what messages are possible, and you don’t need a valid ciphertext to do it.
The first step in this encryption attack is to take the message we want to encrypt using the server’s key, apply padding, and split it into blocks. This will serve as our chosen plaintext. For simplicity, let’s assume our plaintext fits within a single block for now.
Interestingly, the next step is to create the ciphertext for this plaintext block. You might expect generating this ciphertext to be the hard part, but it’s surprisingly straightforward.
In fact, the ciphertext can be anything we want. Yes, really. The real challenge in this attack lies in figuring out the IV that, when XOR’d with the intermediary value produced by our chosen ciphertext, yields the plaintext we want.
Since the ciphertext value doesn’t matter, let’s make it a block full of 0x00 bytes. To begin the attack, we’ll send this ciphertext to the /gamble endpoint along with an IV that’s also all zeros.

Bytes we don't know the value of have question marks.
Here’s what we know so far:
- The ciphertext bytes (a block of zeros).
- The XOR value (an IV of zeros).
What we don’t know yet:
- The intermediary value.
- The plaintext value produced by this ciphertext and IV.
At first glance, this might not seem like much to go on. But as we demonstrated during the decryption attack, brute-forcing each byte of the IV while paying attention to the oracle’s responses will eventually reveal an IV that produces a plaintext made entirely of padding.
So, we’ll go over the brute-forcing process, just like we did on the previous attack, on our zeroed-out ciphertext block. Eventually, we’ll find the IV that produces this:

After performing the brute-force attack, we arrive at a plaintext full of padding.
Now that we’ve discovered the plaintext, we can XOR it with the IV that generated it to uncover the intermediary value, just like we did in the decryption attack:
$$ \text{Plaintext Value} \oplus \text{XOR Value (our IV)} = \text{Intermediary Value} $$At this point, let’s take a step back to reassess:

Now we know the intermediary value.
Now we now know:
- The ciphertext bytes (our block of zeros).
- The intermediary value.
- The plaintext (what we wish our ciphertext to decrypt to).
The final piece of the puzzle is finding the IV that, when XOR’d with the intermediary value, produces our chosen plaintext.
Fortunately, this is simple:
$$ \text{Intermediary Value} \oplus \text{XOR Value (The missing IV)} = \text{Plaintext} $$Reversing the equation lets us calculate the IV directly:
$$ \text{Plaintext Value} \oplus \text{Intermediary Value} = \text{XOR Value (The missing IV)} $$By performing this XOR, we can compute the IV that, when paired with our chosen ciphertext, produces the plaintext we want.

IV revealed!
If we want to encrypt a plaintext that spans multiple blocks, the process is similar but harder to explain. We’ll perform the same steps on each plaintext block, starting with the last block and working backward to the first.
In simpler terms:
- We start with last plaintext block where we’ll use a dummy ciphertext block (all zeros) and figure out the IV that produces the plaintext block we seek.
- For every preceding plaintext block, what would be the IV from the subsequent block (the one previously worked on) serves as its ciphertext. We then figure out the IV like before.
- When the first plaintext block is processed, its IV will be actual IV for the message.
I realize this explanation can be hard to follow in words. Sometimes code is more effective at conveying these concepts. Here’s an excerpt from the encrypt function in the Delphi source code:
def encrypt(plaintext : bytes, oracle : callable) -> tuple[bytes, bytes]:
# Pad the plaintext to ensure it matches the required block size.
plaintext = pad(plaintext, BLOCK_SIZE)
# Split plaintext into blocks.
plaintext_blocks = [plaintext[i:i+BLOCK_SIZE] for i in range(0, len(plaintext), BLOCK_SIZE)]
# Initialize the process by creating a block filled with junk data (zeros in this case).
# This block serves as the final block of the ciphertext, to which additional blocks will be prepended in the loop.
# For the first iteration, this junk block will act as the "previous block".
prev_block = bytearray(BLOCK_SIZE)
result = prev_block
# Encrypt plaintext blocks in reverse order.
for idx, block in enumerate(reversed(plaintext_blocks)):
# Gets the intermediary value for a block full zeros.
zeroing_iv = _get_intermediary_value(prev_block, oracle)
# XOR the zeroing IV and current block to derive the current block's ciphertext.
new_block = bytes(a ^ b for a, b in zip(zeroing_iv, block))
# Prepend the new block to the result being assembled.
result = new_block + result
# Update the previous block to the newly created block for the next iteration.
prev_block = new_block
# The IV is be the first block of the forged ciphertext.
iv = result[:BLOCK_SIZE]
# The remaining blocks are the ciphertext properly.
ciphertext = result[BLOCK_SIZE:]
return iv, ciphertext
With the theory covered, let’s revisit our betting site example. What could an attacker do with the ability to craft valid ciphertexts for any message they choose?
They could forge a token for another user, like the administrator, and deliberately place losing bets, draining the administrator’s funds.
To test this, we can use Delphi’s encrypt function to create our own PoC:
from delphi import encrypt
import base64
import requests
from Crypto.Util.Padding import unpad
# API service
URL = 'http://127.0.0.1:5000'
def ask_oracle(iv : bytes, ciphertext : bytes) -> bool:
token = base64.b64encode(iv + ciphertext).decode('utf-8')
data = { "token" : token, "bet" : "WHATEVER"}
response = requests.post(f"{URL}/gamble", json=data)
if response.status_code == 500:
return False
else:
return True
# Token we wish to forge
plaintext = 'Admin,HEADS'.encode('utf-8')
# Run the attack
iv, ciphertext = encrypt(plaintext, ask_oracle)
# Print forged token
print(base64.b64encode(iv + ciphertext).decode('utf-8'))
Running this PoC will produce a forged token. Using it, we can repeatedly drain the administrator’s wallet until their balance hits zero. Mission accomplished!
[user@mydesktop ~]$ python poc.py
iSzlZFkQroiTuz455gGB+wAAAAAAAAAAAAAAAAAAAAA=
[user@mydesktop ~]$ curl -X POST \
-H "Content-Type: application/json" \
-d '{
"bet": "TAILS",
"token": "iSzlZFkQroiTuz455gGB+wAAAAAAAAAAAAAAAAAAAAA="
}' \
'http://127.0.0.1:5000/gamble'
Better luck next time, Admin!
As we make more bad bets, we can confirm the damage we’re causing on the server logs:
127.0.0.1 - - [13/Dec/2024 09:44:45] "POST /gamble HTTP/1.1" 401 -
Admin lost 10 and now has a balance of 40.
127.0.0.1 - - [13/Dec/2024 09:44:58] "POST /gamble HTTP/1.1" 200 -
Admin lost 10 and now has a balance of 30.
127.0.0.1 - - [13/Dec/2024 09:44:59] "POST /gamble HTTP/1.1" 200 -
Admin lost 10 and now has a balance of 20.
127.0.0.1 - - [13/Dec/2024 09:45:05] "POST /gamble HTTP/1.1" 200 -
Admin lost 10 and now has a balance of 10.
127.0.0.1 - - [13/Dec/2024 09:45:05] "POST /gamble HTTP/1.1" 200 -
Admin lost 10 and now has a balance of 0.
‘A’s In Ciphertext
You might have noticed that the base64 representation of our forged token ends with a series of ‘A’s.
This happens because our final ciphertext block, which is entirely zeros, gets encoded as ‘A’s when converted to a string.
A legitimate ciphertext is highly unlikely to have such a pattern. If a curious administrator were inspecting logs to debug the security issues affecting their online casino, they might stumble across this anomaly and become suspicious.
To avoid drawing attention to your forged ciphertext, consider using a random last ciphertext block instead of one filled with zeros.
Prevention
The root cause of this attack lies in the fact that the target allows users to submit arbitrary ciphertexts to be decrypted and have the plaintext padding removed. It assumes that any ciphertext provided by the user was generated by the server and hasn’t been tampered with. However, as we saw, this assumption is flawed.
At its core, this is an integrity issue. There needs to be a way to distinguish between ciphertexts that are authorized for decryption (those generated by the server) and those that are not (forged by the user).
There are two good options for addressing this:
- Switching from CBC to other modes of operation, such as Galois/Counter Mode (GCM), which includes an authentication tag with the ciphertext.
- If we must stick with CBC, implementing the Encrypt-then-MAC pattern is essential. This involves calculating a Message Authentication Code (MAC) for the ciphertext and sharing it along with the ciphertext and IV. Decryption should only occur if the MAC checks out.
Either of these methods would add an integrity check, preventing tampering with the ciphertext and effectively neutralizing padding oracle attacks.
You might be tempted to try solving this issue with other approaches, like modifying the status code response to eliminate the oracle or adding rate-limiting to the endpoint to slow down brute-force attacks. However, the reality is that this is a cryptographic vulnerability, and anything other than a cryptographic solution will fail to properly address the issue.
Credits & Resources
This post would not have been possible without the some very smart people on the internet who explained this attack on their own blogs and websites.
If you’re still unclear about some aspects of the attack, I highly recommend checking out these resources, which I found incredibly helpful when researching this topic:
Cryptopals: Exploiting CBC Padding Oracles
An excellent explanation of the decryption attack. The Python code provided also heavily inspired the creation of Delphi.
Going the Other Way with Padding Oracles: Encrypting Arbitrary Data!
The best source online for encryption padding oracle attacks. Seriously, there’s a lot of misinformation about this topic.
Automated Padding Oracle Attacks with PadBuster
The most comprehensive explanation of the decryption attack I could find, though the encryption part leaves a bit to be desired. You should also check out their tool for exploiting padding oracles, PadBuster.
Testing for Padding Oracle
OWASP’s resource for detecting this vulnerability from a black-box and gray-box testing perspective.
Big thanks to Parminder Singh, who read the article and reached out to me about a mistake in my explanation, where I had assumed that:
$$ \text{if A} \oplus \text{B} = \text{C} \text{, then A} \oplus \text{B+1} = \text{C+1} $$This, is of course, not how XOR operations work (don’t know what I had in mind when I wrote that, since this is not how I implemented the attack in code).
